無論國考還是聯考、四川省公務員考試，不定方程是數學運算歷年考查的重點題型，也是令很多考生畏懼的難點題型。下面以近幾年的省考真題為例，對不定方程這一模塊常用的方法進行詳細的真題解析與命題趨勢分析，以備考生需要。

　　題型一：代入排除法

　　【例1】1分、2分和5分的硬幣共100枚，價值2元，如果其中2分硬幣的價值比1分硬幣的價值多13分，那么三種硬幣各多少枚?( )

　　A.51、32、17 B.60、20、20

　　C.45、40、15 D.54、28、18

　　【解析】不定方程最基本的方法是代入排除法。本題中將選項代入，發現只有A選項滿足2分硬幣的價值比1分硬幣的價值多13分。所以，本題答案為A選項。

　　【練習】裝某種產品的盒子有大、小兩種，大盒每盒能裝11個，小盒每盒能裝8個，要把89個產品裝入盒內，要求每個盒子都恰好裝滿，需要大、小盒子各多少個?( )

　　A. 3，7 B. 4，6

　　C. 5，4 D. 6，3

　　【解析】思路與例1完全相同，直接代入選項，只有A選項滿足89個產品。

　　題型二：數字特性法

　　近來比較喜歡考查在不定方程的基礎上，外加一個條件，這個條件可以是明顯的條件或者暗含在題干信息中。對于此種類型的不定方程，優先考慮奇偶特性，然后考慮尾數特性。

　　【例2】某兒童藝術培訓中心有5名鋼琴教師和6名拉丁舞教師，培訓中心將所有的鋼琴學員和拉丁舞學員共76人分別平均地分給各個老師帶領，剛好能夠分完，且每位老師所帶的學生數量都是質數。后來由于學生人數減少，培訓中心只保留了4名鋼琴教師和3名拉丁舞教師，但每名教師所帶的學生數量不變，那么目前培訓中心還剩下學員多少人?( )

　　A.36 B.37

　　C.39 D.41

　　【解析】假設每名鋼琴老師帶的學生數是x，拉丁舞老師帶的學生數為y，則本題就是在不定方程5x+6y=76

　　的基礎上，加了x、y都是質數這個條件，要根據數字特性來尋求滿足該不定方程的解。先考慮奇偶特性，76是偶數，6y是偶數，則5x是偶數，而5是奇數，所以x是偶數，并且是質數，因此x=2，代入方程，y=11。所以4×2+3×11=41，本題選擇D選項。

　　【練習】超市將99個蘋果裝進兩種包裝盒，大包裝盒每個裝12個蘋果，小包裝盒每個裝5個蘋果，共用了十多個盒子剛好裝完。問兩種包裝盒相差多少個?( )

　　A.3 B.4

　　C.7 D.13

　　【解析】此題與例2屬于同一類型。假設大、小包裝盒的個數分別為x、y，在不定方程12x+5y=99的基礎上，加了一個條件10

　　題型三：賦0法 或者消元法

　　三元一次不定方程組，在求解一個式子的類型中，可以將其中一個未知數賦為0，或者消掉一個未知數，從而轉化為二元一次方程來求解。

　　【例3】甲、乙、丙三種貨物，如果購買甲3件、乙7件、丙1件需花3.15元，如果購買甲4件、乙10件、丙1件需花4.20元，那么購買甲、乙、丙各1件需花多少錢?( )

　　A.1.05元 B.1.40元

　　C.1.85元 D.2.10元

　　【解析】假設甲、乙、丙1件的價錢分別為x、y、z，則根據題意，可以列得不定方程組為：

　　公務員行測備考：必考不定方程 src="http://img.wangxiao.cn/files/RemoteFiles/20140127/868375001.gif">

　　，本題要求的x+y+z的值，而此值為定值。所以可以賦y=0，則解得x=1.05，z=0，則x+y+z=1.05，答案為A選項。本題也可以采用消元法，將第一個方程×3-第二個方程×2=x+y+z=1.05。

　　【練習】甲買了3支簽字筆、7支圓珠筆和1支鉛筆，共花了32元，乙買了4支同樣的簽字筆、10支圓珠筆和1支鉛筆，共花了43元。如果同樣的簽字筆、圓珠筆、鉛筆各買一支，共用多少錢?( )

　　A.21元 B.11元

　　C.10元 D.17元

　　【解析】本題與例3屬于同一類型。假設1支簽字筆、圓珠筆、鉛筆的價錢分別為x、y、z，可以列得不定方程組為：

　　公務員行測備考：必考不定方程 src="http://img.wangxiao.cn/files/RemoteFiles/20140127/868375002.gif">

　　，本題要求x+y+z的取值，此值為定值。所以賦y=0，則解得x=11，z=-1，則x+y+z=10。本題也可以采用消元法，將第一個方程×3-第二個方程×2=x+y+z=10。答案為C選項。

　　題型四：特殊因子法

　　三元一次不定方程，求解的不是一個式子的時候，可以采用特殊因子法。

　　【例4】某公司的6名員工一起去用餐，他們各自購買了三種不同食品中的一種，且每人只購買了一份。已知蓋飯15元一份，水餃7元一份，面條9元一份，他們一共花費了60元。問他們中最多有幾人買了水餃?( )

　　A.1 B.2

　　C.3 D.4

　　【解析】假設蓋飯、水餃、面條各購買了x、y、z份，則根據題意有：

　　

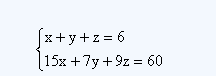
　　，根據第二個方程15x、9z、60都是3的倍數，所以7y也是3的倍數，y是3的倍數，又是小于6的整數，因此y=3，本題答案為C選項。

　　【小結】

　　不定方程的主要方法不外乎五類：代入排除法、數字特性法、賦0法、消元法、特殊因子法，五種方法并不具有排他性，也可結合起來使用。基本題型分四種：

　　1. 題目如果只列不定方程或者不定方程組，沒有給定顯性條件，則優先考慮代入排除法;

　　2. 題目如果只列二元一次不定方程，外加條件，一般考慮數字特性法：優先奇偶特性，然后考慮尾數特性;

　　3. 題目如果是三元一次不定方程組，求解一個為定值的式子，則用賦0法 或者消元法;

　　4. 題目如果是三元一次不定方程組，求解一個未知數，則可以用特殊數字法。

（責任編輯：中大編輯）